No blog post in 2014! I have yet written a lot.

In this post, I want to explain in a few minutes how does Lightweight Modular Staging (LMS) work.

Essentially, LMS is a Scala library for generating programs. The basic idea is that you define an abstract representation of the program you want to generate and then you apply a code generator on it to produce the target program.

A composable way to define programs

In the same way that you can write complex programs by combining simpler program parts, you can define complex representations of programs by combining representations of simpler program parts. Let’s see how you can define simple program representations and then how to combine them.

An example of simple program is a program that just returns the value “1”:

val one = unit(1)

The unit fonction takes a value as parameter and returns a representation of a program whose result is this value. Here, one is a representation of a program that returns the Int value “1”. Similarly, unit("foo") gives a representation of a program that returns the String value “foo”.

Concretely, programs are represented by graphs of abstract expressions, where nodes are expressions and edges are dependencies between them. In the above example, one is a graph made of just one node, Const:

Let’s see how you can combine representations of programs to get representations of more complex programs:

val one = unit(1)
val two = unit(2)
val three = plus(one, two)

Here, plus is a function that takes as parameters two representations of programs returning numeric values and returns a representation of a program that returns their sum:

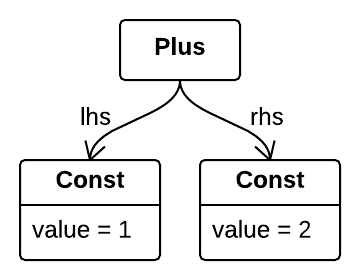
Rep[A]

Note that you don’t need to know the internal representation of programs to be able to use LMS. I’m showing them just for pedagogical purposes. (By the way, my figures show only an approximation of the real internal representation used by LMS. But you get the idea.)

Actually, as a user of LMS, the only type you see is Rep[A], which means “representation of a program that returns a value of type A”. For instance, one has type Rep[Int], unit("foo") has type Rep[String] and Rep[Seq[Boolean]] is the type of representations of programs returning a sequence of booleans.

It is worth noting that the Rep[A] type provides no operations, it is just defined as follows:

type Rep[A]

The purpose of this type is just to track the return type A of the represented programs so that you combine them in a correct way. For instance plus(one, unit("two")) does not compile because unit("two") is a program returning a String value (i.e. it has type Rep[String]).

Generating target programs

Your ultimate goal is to execute your programs. Once you have defined a program as explained above, the next step consists in generating code for it. A code generator essentially visits a program’s abstract representation and produces the code corresponding to each node.

As an example, here is the relevant part of a JavaScript code generator for the Plus node:

case Plus(lhs, rhs) => gen"var $sym = $lhs + $rhs;"

The code generator emits code that generates a statement corresponding to the definition of a variable containing the result of the expression represented by the Plus node.

When we run the JavaScript code generator on the three program representation, it produces the following code:

var x0 = 1 + 2;

Syntactic sugar

Until now the way of writing program generators may seem cumbersome, even on the very simple example I gave. Fortunately, you don’t actually need to write as many characters as did in my above examples. Let’s illustrate this with a simple example, a function inc that takes as parameter a program returning an Int value and returns a program returning this value incremented by one:

def inc(n: Rep[Int]) = plus(n, unit(1))

For comparison, here is how you would write a program equivalent to the above program generator:

def inc2(n: Int) = n + 1

This version is much easier to read, because it uses the symbolic operator “+” directly with the literal term “1”. The good news is that inc can be re-written so that its body is exactly the same as inc2:

def inc3(n: Rep[Int]) = n + 1

It works because LMS provides an implicit conversion defining a + operator on Rep[Int] values, and an implicit conversion turning any value into a representation of a constant program returning this value.

A vs Rep[A]

Don’t be confused, the + in inc3 is not the same + as in inc2, even though the symbols are the same. In inc2 it takes two numbers and returns their sum, whereas in inc3 it takes two programs and returns a program that returns their sum. The compiler knows to which + your code refers to because of the types of your terms (Int in inc2 vs Rep[Int] in inc3).

In fact, one of the goals of LMS is to allow you to define your program generators with the same syntax as your programs, excepted that your terms have type Rep[A] instead of A.

Trying to support the same syntax for two things that are not really the same may sound like a dubious idea to you, but it is actually totally relevant. Indeed, even though inc2 and inc3 are technically two completely different guys, they both define the same computation: adding one to a number.

Now consider these two expressions: inc2(42) and inc3(42). Both define computations that add 1 to 42. The key difference between them is not what they compute but when these computations happen. In the former case, the computation happens when you evaluate the expression, whereas in the latter case the computation happens when you evaluate the target program.

So, the key difference between A and Rep[A] terms is that the evaluation of the latter is delayed.

In a sense, when you evaluate your program generator, you partially evaluate your target program because you immediately evaluate the A terms and delay the evaluation of the Rep[A] terms.

Perspectives

You might be wondering what could be the purpose of delaying the evaluation of computations instead of directly evaluating them. The answer lies in one term: performance. Indeed, the high-level abstractions of your program generator can be partially evaluated to produce a more specialized and therefore more efficient target program. This topic is, however, out of the scope of this post. If you want to know more about LMS, I invite you to have a look at https://scala-lms.github.io and to give it a try.